There is no better game for a peaceful Saturday evening than Minecraft. You can explore, build, fight monsters or tunnel your way through endless stone while watching math videos from YouTube. Thanks 3Blue1Brown for an excellent Fourier Transform video)!
Inspired by math and data science I wanted to optimize my diamond yield (most valuable mineral in the game). The topic has really been over-analyzed already. My inspiration came from this post on Reddit /r/Minecraft showing odd streaks along the z-axis. Nevertheless, I wanted to see what I could discover on my own.
I started a Jupyter Notebook and searched the Internet for how to read a Minecraft .mca -file. Of course, other people had already done work on this topic years ago, so it didn’t take too long to find a great source and a Python implementation for getting the data.
The area under examination was 1775 chunks from a world where I have ran around slightly generate more chunks. 16×16 chunks that can have a height between 63 and 255 (minimum comes from the sea level) is minimum of 28 627 200 blocks. Because Minecraft does’t save empty chunks of just air, my dataset had 39 870 463 data points.
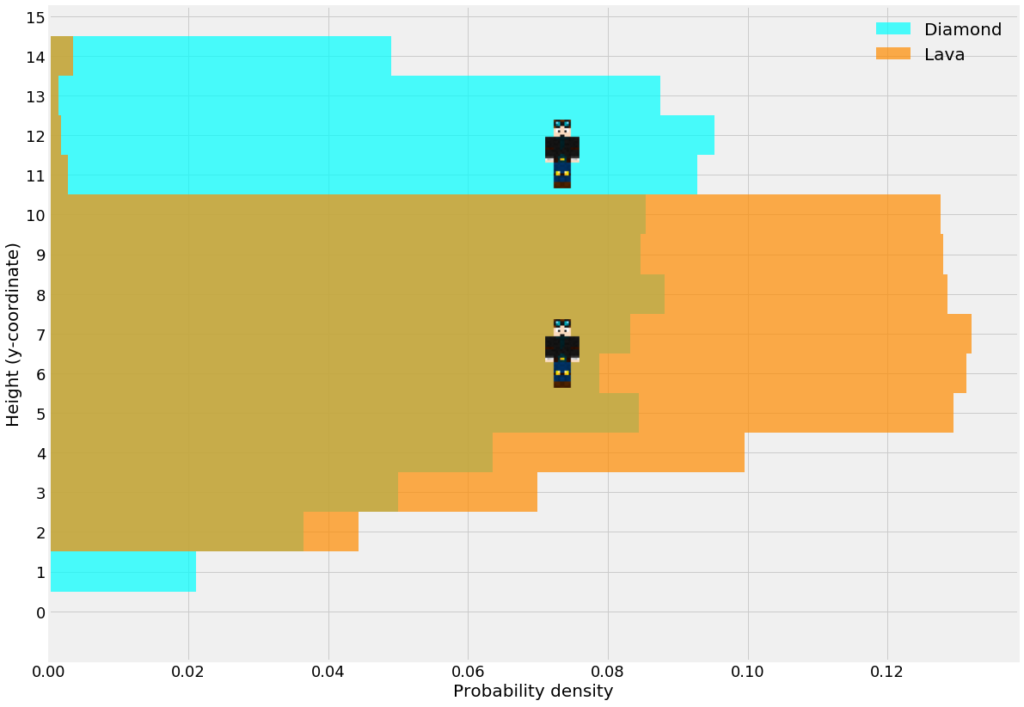
Based on what I found, I will be mining mainly on level 11 and sometimes at level 6. This maximizes the visibility to high density blocks also above and below me. It might be fastest to ignore the diamonds on level 6 due to high concentration of lava lakes which can easily be bridged over at level 11.
Running on 8 GB of RAM, I found myself running out of memory more than once, so I looked up tips for working with a large dataset using the Python library pandas. I also skipped stone and air as their distribution is not that interesting or relevant. Skipping those most frequent but irrelevant blocks dropped my memory consumption from over 700 MB to 110 MB. Of course, I could skip most of the blocks but I was exploring the data so I wanted to see as much as possible.
On their own, my results are not very significant considering the amount of different Minecraft world that could be generated randomly and the relatively small amount of chunks inspected. So my work assumes that the distribution of diamonds is uniform across random worlds and independent of other variables such as the biome in which they appear.
As next steps, I could take a look at the distribution of other minerals. I’m starting a University course in Information Visualization next month and look forward to graduating to real world datasets.